研究概要

中静研究室では，音声や画像を対象とした信号処理の研究を行っている． 当研究室では，信号を表すためのモデルを構築し，そのモデルを信号から推定する過程で，さまざまな信号処理・音声処理・画像処理の問題を解く研究を行っている． モデルを推定することは，人間の知覚における学習と類似した過程である． 画像や音声・音響信号に対する学習能力を計算機上に構築することで，従来の信号処理システムを凌駕し，人間の能力を超える計算知覚を実現することを目標としている．

加算と最大値・最小値演算による熱拡散方程式の離散化と深層ネットワーク

熱拡散方程式は，熱の時間発展を表す偏微分方程式である． 画像処理の分野では，画像の平滑化などへ応用されてきた． この研究では，偏微分方程式に現れるラプラシアンを加算と最大値演算だけで構成されるモフォロジカル演算(最近ではトロピカル代数と呼ばれることも)で離散化し，パラメータを持つ非線形演算を拡張，さらに反復演算を深層展開することで深層ネットワークを構築した． 低精度数値表現で画像処理が実行でき，かつニューラルネットワークにおける隠れ層が画像1枚分で済む特徴から，下図のビデオでは，クロック周波数200MHzのARM Cortex M4，192KBのRAMでガウス性ノイズ除去を達成している．(マイコンは WIO Terminal . 内部では8ビット演算であるが，ディスプレイのハードウェアの制限から出力は32階調)


参考文献:
1. G. Okada and M. Nakashizuka, ``Deep unrolling of diffusuion process with morphological Laplacian and its implementation with SIMD instructions, ‘’ Proc. 2022 IEEE International Conference on Image Processing, pp. 2931 - 2934, Bordeaux, Oct. 2022.
2. G. Okada and M. Nakashizuka, ``Deep Unrolling of  Non-Linear Diffusion with Extended Morphological Laplacian,'' IEICE Trans. of Fundamentals, vol. E106-A, no. 11, pp. 1395--1405, Nov. 2023.

深層モフォロジカルフィルタによるガウス性ノイズ除去ネットワーク

ガウス性雑音除去のためにモフォロジカルフィルタの線形結合に基づく深層ネットワークを提案した． モフォロジカルフィルタの応用の一つにトップハット変換がある． これは，画像の輝度の極値の近傍を抽出する方法である．このトップハット変換を利用して，雑音成分を取り出し，これを繰り返し画像から引き算する構造から深層ネットワークを構築した． モフォロジカルフィルタは，画像の加算と最大・最小の計算から実現することができるため，ほとんどの計算を8ビット符号無し整数で実現することができる． この性質から，ARMプロセッサのSIMD命令を利用することで，Raspberry Pi 3にネットワークを実装，1秒程度の計算時間で512x512画素の雑音除去を実現した． BM3Dと同程度の雑音除去能力を維持しながら，フルサイズの畳み込みニューラルネットワークよりも大幅にメモリ容量，計算時間を削減することができた． (Raspbery Piで実行できるソースコードはhttps://github.com/Nkszk/Pymorph )


mnet.png(270,789 byte)
参考文献:
1. H. Fujisaki and M. Nakashizuka, ``Deep morphological filter networks for gaussian denoising,'' in Proc. 2020 IEEE Int'l Conf. on Image Processing, pp. 918-922, Abu Dhabi, Oct. 2020.
2. H. Fujisaki, M, Nakashizuka, ``Deep Gaussian denoising network based on morphological operators with low-precision arithmetic, '' IEICE Trans. on Fundamentals, Vol.E105-A,No.4, Apr. 2022.

凸フィルタネットワークによる印刷文字と手書き文字の分離・抽出

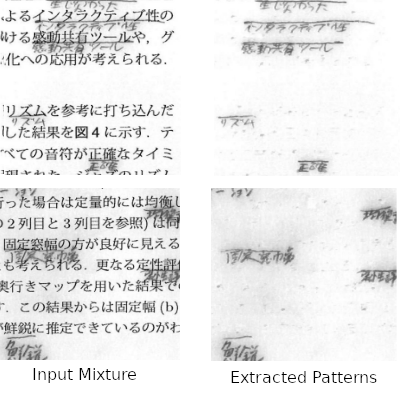
先に提案した凸フィルタネットワークを用いることで，活字上にオーバーラップした手書き文字を抽出する方法を提案した． 印刷文字の局所的な構造を2層の凸フィルタネットワークに学習させることで，手書き文字のみを残して活字だけを除去することができた． メモ付きの印刷文章から，メモだけを抽出しアーカイブするなどの応用が考えられる．


hp.png(270,789 byte)
参考文献:
1. K. Itoi and M. Nakashizuka,``An extraction method of handwritten characters on printed documents by maxout filter networks, '' in Proc. Int'l Symp. on Intelligent Signal Processing and Communication Systems, Ishigaki, Nov. 2018.
2. 糸井清晃, 中静　真,``Maxoutフィルタネットワークによる印刷文書上の手書き文字の抽出, '' 画像電子学会誌, vol.　48, no. 1, pp. 144-152, 2019年2月

凸フィルタ・凹フィルタネットワークの学習と画像処理応用

ニューラルネットワークの活性化関数の一つとして Maxoutが提案されている． Maxoutは，任意の凸関数を線形区分凸関数で近似することができる．Maxoutを活性化関数とする畳み込み型ニューラルネットワークは，モフォロジカル画像処理の分野におけるダイレーション(膨張)の拡張であることに着目し，モフォロジカルフィルタの構造を基に畳み込み型ネットワークを構成する方法を提案した．参考文献ではダイレーションとエロージョンを，それぞれMaxoutにより，入出力の関係が凸関数で記述される凸フィルタ・凹関数で記述される凹フィルタへ拡張し，クロージングフィルタから，凸凹フィルタを構成した．下図には，凸凹フィルタを訓練することで，画像のブラインドマスク除去へ応用した例を示している．この研究で提案した拡張は，さまざまなモフォロジカル画像処理を，学習可能な深層ネットワークへと拡張できることを示している．


maxout.png(270,789 byte)
参考文献:
1. M. Nakashizuka, K. Kobayashi, T. Ishikawa, K. Itoi, ``Convex filter networks based on morphological filters and their application to image noise and mask removal, '' IEICE Trans. on Fundamentals, vol. E100-A, no. 11, pp. 2238--2247, Nov. 2017.
2. M. Nakashizuka, K. Kobayashi, T. Ishikawa, K. Itoi, ''Maxout filter networks referencing morphological filers, '' Proc. EUSIPCO 2017, pp. 1649 - 1653, Kos, Aug. 2017.

モフォロジカル勾配によるL1-L∞ノルム正則化

マセマティカルモフォロジーは，集合演算に基づく画像処理の体系的な手法である．パターン認識の分野において特徴抽出法として用いられている細線化，太線化の一般化と捉えることもできる．細線化に相当する操作をエロージョン(侵食), 太線化に相当する操作をダイレーション(膨張)と呼ぶ．ダイレーションとエロージョンの差は，モフォロジカル勾配と呼ばれ，輝度勾配の近似となる．当研究室では，モフォロジカル勾配が，差分の集合のL∞ノルムであることに注目し，画像のL1-L∞ノルムによる正則化を提案した．L∞ノルムの性質から，構造要素(最大値・最小値を求める範囲)のサイズにより，画像の細部を保存できる平滑化を実現した．下に示す画像は，左から原画像，サイズ2，サイズ4,サイズ8の平滑化画像である．平滑化画像の二乗誤差はすべて同じであるにもかかわらず，細部の再現性がサイズに依存して変化していることがわかる．この性質から，提案法は，画像の構造の解析，特徴抽出等に利用することが期待できる．


mg_smoothing.png(43436 byte)

また，構造要素のサイズに依存して原画像の細部を保存できる性質を利用し，画像を骨格成分とテクスチャへ分離，それぞれに異なるペナルティを課すことで，従来のTV正則化よりも高精度かつテクスチャ保存に優れた雑音除去を達成した．


mg_decomp.png(43436 byte)
参考文献:
1. M. Nakashizuka, ``Image regularization with higher-order morphological gradients, '' in Proc. EUSIPCO 2015, Nice, Aug. 2015.
2. M. Nakashizuka, ``Image regularization with multiple morphological gradient priors, '' in Proc. IEEE Int'l Conf. on Image Processing, Phoenix, Sept. 2016.

モフォロジー画像表現と画像復元への応用

画像がモフォロジー演算で合成されることを事前情報として，雑音重畳などにより劣化した画像から，雑音に隠れた原画像を復元する問題に取り組んでいる． 下記の例では，超低SN比の画像(QRコード)より，画像そのものが細かなブロックの和から構成されていることを事前知識として雑音の除去を行った例である． 逆問題の解法である正則化法と，集合論の応用であるマセマティカルモフォロジーを融合させることを目標としている．


recovery.png(43436 byte)
参考文献:
1. M. Nakashizuka, S. Takenaka and Y. Iiguni, ``Learning of structuring elements for morphological image model with a sparsity prior, '' in Proc. IEEE Int'l Conf. on Image Processing, Hong Kong, Sep, 2010.
2. 西野洋一, 中静 真, 花田良子, 棟安実治, 飯國洋二, ``最大・最小値の近似に基づくモルフォロジフィルタの設計法, '' 電子情報通信学会A, vol. J93-A, no. 9, pp. 594-604, 2010年9月
3. M. Nakashizuka, Y. Ashihara and Y. Iiguni, ``Morphological regularization for adaptation of image opening, '' in Proc. EUSIPCO 2011, Barcelona, Aug. 2011.
4. M. Nakashizuka, Y. Ashihara and Y. Iiguni, ``An adaptation method for morphological opening filters with a smootheness penalty on structuring elements, '' IEICE Trans. on Fundamentals, vol. E96-A, no. 6, Jun. 2013.
5. M. Nakashizuka, ``Image recovery with soft-morphological image prior, '' IEICE Trans. on Fundamentals, vol. E97-A, no. 12, pp. 2633-2640, Dec. 2014.

画像のスパース分解と特徴抽出 -基底系学習-


Texture.png(43436 byte)

多くの画像解析手法では，画像を構成する要素をあらかじめ仮定し，決められた要素を画像から抽出することが基本となる． 例えばエッジ検出では，抽出したいエッジの形状に合わせてフィルタを設計する． また，信号解析法として良く用いられるウェーブレット解析では，画像の構成要素がウェーブレット基底と類似することが前提となっている．

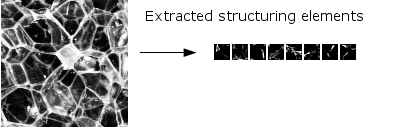
それらに対して，中静研究室では，画像の特徴を表す構造が，"まばら"に発生することを仮定するだけで，事前情報を用いずに構成要素を学習するアルゴリズム:シフト不変スパースコーディングの研究を行った． 上図は，テクスチャ画像の中から特徴的な構造を自動的に抽出した例である． 下図は，欠損の発生した画像から，繰り返される構造を推定し，劣化前の画像を復元した例である． 人間の知覚では，原画像のテクスチャを類推できない領域が発生しているにもかかわらず，繰り返される画像構造を劣化画像から推定することで，良好な欠損の復元を達成している．


50.png(462180 byte)

75.png(462180 byte)
参考文献
1. M. Nakashizuka, H. Nishiura and Y. Iiguni, ``Sparse image representations with shift-invariant tree-structured dictionary, '' in Proc. IEEE Int'l Conf. on Image Processing, Cairo, Nov, 2009.
2. M. Nakashizuka, H. Nishiura, Y. Iiguni, ``Shift-invariant sparse image representations with tree-structured dictionary, '' IEICE Trans. on Fundamentals, vol. E92-A, no. 11, pp. 2809-2818, Nov. 2009.

信号源のモデルに基づくスパース信号分解と単一チャネル音声分離問題への応用


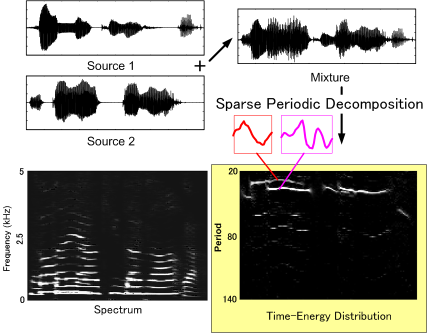
SPD.png(64907 byte)

混合された音から，個々の音源を分離する問題は，音源分離問題と呼ばれ，音声認識，音楽の解析等，多くの応用が期待されている． 多くの音源分離法では，複数のマイクロホンを用い，音源の位置の違いによって分離を達成している． それに対して，中静研究室では，単一のマイクロホンのみを用いた複数話者の音声分離，雑音除去等の検討を行っている． 音源分離のために，混合されている波形のモデルを作り，そのモデルが混合中に"まばらに"存在することを仮定することで信号分解を行うアルゴリズム:スパース周期信号分解法を提案した． スパース周期信号分解により，混合音声は，わずかな数の周期信号群へと分解される． 分解結果にクラスタリングを適用し，さらにクラスタを話者情報をもとに話者へ振り分けることで音声分離を達成している．

参考文献
1. M. Nakashizuka, "A sparse decomposition method for periodic signal mixtures, " IEICE Trans. on Fundamentals, vol. E91-A, no. 3, pp.791-800, March 2008.
2. M. Nakashizuka, H. Okumura and Y. Iiguni, ``A sparse periodic decomposition and its application to speech representation, '' in Proc. on EUSIPCO 2008, Lausanne, Aug. 2008.
3. M. Nakashizuka, H. Okumura and Y. Iiguni, ``Single-channel speech separation by using a sparse periodic decomposition, '' in Proc. EUSIPCO 2009, Glasgow, Aug. 2009.
4. M. Nakashizuka, H. Okumura and Y. Iiguni, ``Supervised single-channel speech separation via sprse decomposition using periodic signal models, '' IEICE Trans. on Fundamentals, vol. E95-A, no. 5, pp. 853-866, May 2012.

モフォロジー演算を用いた画像形状処理とその応用


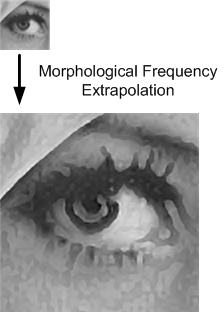
Morph.png(46681 byte)

マスマティカルモルフォロジと呼ばれる集合演算に基づく図形処理の研究を行っている． 図に示した例では，画像中の輪郭がステップ上の輝度変化で近似できることを利用することで，モルフォロジ演算により拡大画像の輝度変化を強調した例である． 双三次補間法では補うことのできない画像の高周波成分を生成することが可能であり，さらに，アンシャープマスキング等の画像強調で発生する輝度のオーバーシュート，アンダーシュートを抑えつつ画像拡大を実現している．


参考文献
M. Shimizu, M. Nakashizuka, Y. Iiguni, "Image enlargement by nonlinear frequency extrapolation with morphological operators, " IEICE Trans. on Fundamentals, vol. E91-A, no. 3, pp.859-867, March 2008.